はじめに:短絡容量と短絡電流
高圧需要家の電気設備設計において、短絡容量の選定は、単なる機器スペックの決定を越えた、事故時の波及的被害を防ぐための「最後の砦」を築く作業に他なりません。電気設備設計者が最も神経を使うべきこのテーマについて、実務的な視点からその深層を紐解いていきましょう。
短絡容量の計算を誤ると何が起こるのかという基本から、どのように計算すれば良いかを電験の勉強に絡ませながら理解し、実務レベルに理解を引き揚げます。この記事を読むことで、まだ短絡容量の意味が分からずに困っている初心者設計者の方は、確実に実務者として十分な基礎力を手にすることが出来ます。
本記事内で「短絡容量」と呼んでいるのは、原則的に[MVA]で表されるものをイメージしがちですが、VCBやブレーカ等の遮断器のカタログにおいては、「(短絡)遮断容量[kA]」と言う用語もありますのでご注意ください。こちらは「電流値」です。「容量」と呼ぶのに単位が kVA や MVA でないのに違和感をずっとT係長は覚えているのですが、一般的な用語です。専門的には、電圧(kV)×電流(kA)×√3 で算出される短絡容量(MVA)を基準にする考え方と、実際の遮断能力としての電流値(kA)を混同して呼ぶ慣習があるのがその原因でしょう。単位を確認しなかがら読むと整理できます。
短絡遮断容量選定の重要性と受電点短絡容量の真意
高圧受電設備において、万が一短絡事故が発生した際、その回路には定格電流の数十倍から数百倍という凄まじいエネルギーを持った電流が流れ込みます。高圧受電設備のVCBや断路器などの多くは 12.5kA の短絡容量となっています。これは、電力会社側で受電点の短絡容量を 12.5kA 以下にしなければならないと規定されているからです。事故時の巨大な短絡電流を安全に遮断し、設備へのダメージを最小限に抑えるために不可欠なのが、遮断器の「短絡遮断容量[kA]」です。そして、この選定の起点となるのが、電力会社から提示される (受電点)短絡容量[%] (基準容量10[MVA])です。いろいろと新しい言葉が登場するので、順に解説をしていきます。
電気技術者必須の %Z(パーセントインピーダンス) と 短絡電流 \( I_s \)
受電点短絡容量[%]を理解するには、まずは電験でもおなじみの %Z(パーセントインピーダンス) を理解しなければなりません。私たちの携わる電気設計の現場でこの言葉を聞かない日はありません。しかし、その正体を直感的に説明するのは意外と難しいものです。実務的な定義を一言で言えば、「電圧降下を割合として示したもの」、言い換えると「電気の通りにくさを割合として示したもの」です。まずはイメージだけ持っておきましょう。
この数値が持つ最大の役割は、事故時における「ダムの放水制限」のような機能にあります。%Z が小さいほど、平常時の電圧降下は抑えられ効率は良くなりますが、いざ短絡事故が起きた際には、堰を切ったように巨大なエネルギーが流れ込みます。逆に %Z が大きければ、事故時の電流は抑えられますが、平常時の電圧変動が大きくなるというトレードオフの関係にあります。そして、本記事の目的である「短絡電流」の基本式は
\( I_s = \displaystyle\frac{100}{\% Z} \times I_n \)
と定義されます。\( I_n \) は定格電流です。そして、分母にある \( \% Z \) こそが事故電流の大きさを支配しているものだと分かります。
過去問題で確認!電験三種 2025年上期 電力 問16(改)
なかなかイメージが掴みにくいところだと思いますので、電気設備設計者にはおなじみの電験三種の過去問題を題材に理解を深めましょう。電験三種を取得していなくても設計の実務に支障は無いかもしれませんが、やはり資格試験には業界の基礎知識が詰まっていますので、ご自身の業務に関わる分野に関しては、一読することをT係長はおススメしています。
変電所に設置された一次電圧 66kV、二次電圧 22kV、容量 50MVA の三相変圧器に、22kV の無負荷線路が接続されている。その線路が、変電所から負荷側 500m の地点で三相短絡を生じた。
三相変圧器の結線は、一次側と二次側が Y-Y結線となっている。
ただし、一次側からみた変圧器の1相当たりの抵抗は 0.05Ω、リアクタンスは 7Ω、故障が発生した線路の1線当たりのインピーダンスは (0.20+j0.45)Ω/km とし、変圧器の一次側の線路インピーダンス及びその他の値は無視するものとする。
次の(a)及び(b)の問いに答えよ。(a) 事故地点から見て上位側の %Z[%] を求めよ。基準容量は 10MVA とする。
(b) 短絡電流の値[kA]を求めよ。
スポンサーリンク
公式として覚えてしまっている方も多いとは思いますが、定義から導き方を理解しておく方が重要です。あくまでも前述したように「電圧降下の(相電圧に対する)割合」であること、電気の基本は「オームの法則」であることを念頭に置けば簡単です。
\( \displaystyle\frac{V}{\sqrt{3}} = I_n \times Z \) ※Vは線間電圧です。
相電圧に対する割合なので、E(相電圧)で割ります。100倍すればパーセント表示です。
\( \% Z = \displaystyle\frac{I_n \times Z}{E}\times 100 \)
\( \% Z = \displaystyle\frac{I_n \times Z}{\frac{V}{\sqrt{3}}}\times 100 \)
\( \% Z = \displaystyle\frac{\sqrt{3} I_n \times Z}{V}\times 100 \)
右辺の分子と分母にV(線間電圧)を掛けます。基準容量Pで表したい意図です。
\( \% Z = \displaystyle\frac{\sqrt{3}V \times I_n \times Z}{V^2}\times 100 \)
\( \% Z = \displaystyle\frac{P_B \times Z}{V^2}\times 100 \)
基準容量、線間電圧は問題文に与えられていますので、後は Z[Ω]値を求めればOKです。下図の通りです。変圧器のインピーダンスは一次側からみたものなので、事故点である変圧器二次側からみた値に換算しなければなりません。この作業がとても面倒なので、実務では 10MVA 換算された %Z が用いられるのです。
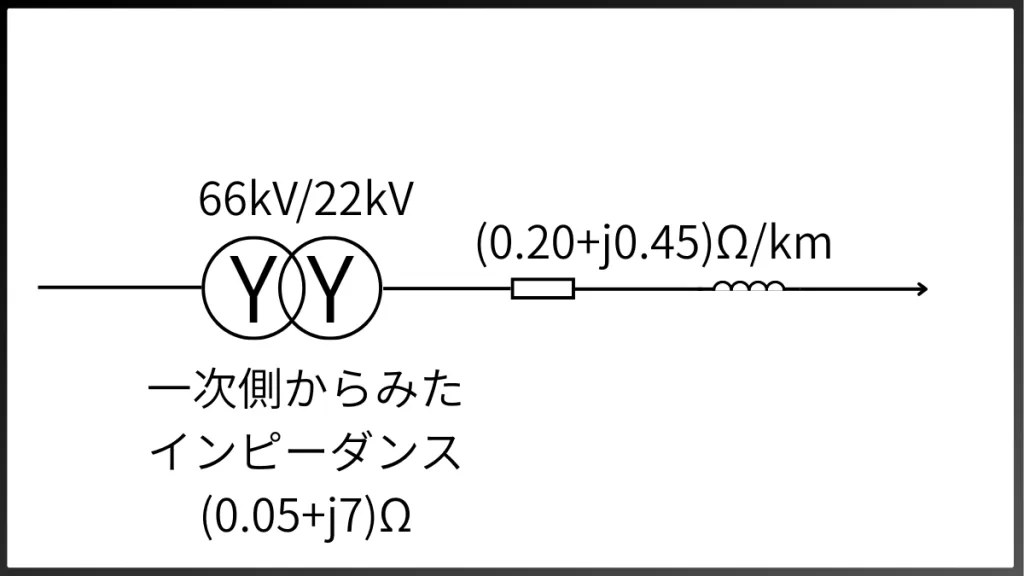
変圧比 \( a = \displaystyle\frac{N_1}{N_2} \) とすると、\( Z_2 = \displaystyle\frac{Z_1}{a^2} \) で表されます。
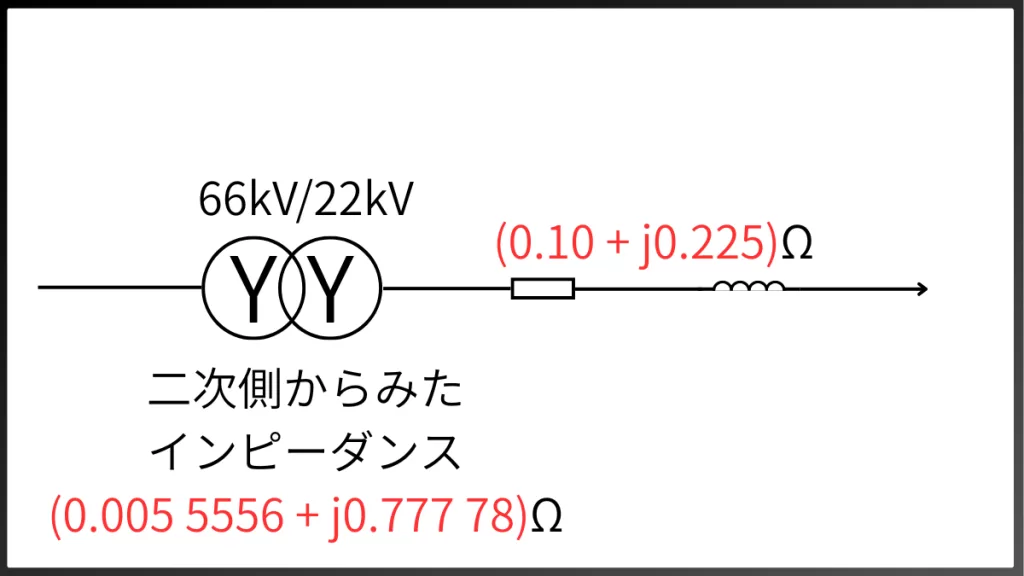
\( \dot{Z} = (0.05 + j7)\times(\displaystyle\frac{22}{66})^2 + (0.20 + j0.45)\times\displaystyle\frac{500}{1000} \)
\( \dot{Z} = (0.005 5556 + j0.777 78) + (0.10 + j0.225) \)
\( \dot{Z} = 0.10556 + j1.00278 \)[Ω]
\( Z = \sqrt{0.10556^2 + 1.00278^2} \)
\( Z = 1.00832 \)[Ω]
従って求める %Z[%] は
\( \% Z = \displaystyle\frac{10 \times 10^6 \times 1.00832 }{22000^2}\times 100 \)
\( \% Z = 2.08331 = 2.08 \)[%] …(答)
前述のとおり \( I_s = \displaystyle\frac{100}{\% Z} \times I_n \) ですから、
\( I_s = \displaystyle\frac{100}{2.08331} \times I_n \)
ここで、\( I_n = \displaystyle\frac{P_n}{\sqrt{3}V} \) より ※容量の基本式
\( I_s = \displaystyle\frac{100}{2.08331} \times \displaystyle\frac{10\times 10^6}{\sqrt{3}\times 22000} \)
\( I_s = 12596.87429 \)[A]
\( I_s = 12.6 \)[kA] …(答)
一見すると、12.5kA 以上となっているように見えますが、事故点はあくまでも送電線 500m 地点です。実際には 500m はおそらく変電所内の送電線です。最も近くの需要家が 1km 地点にあるとして、同様に短絡遮断容量を考えて見ましょう。
\( \% Z = \displaystyle\frac{10 \times 10^6 \times \sqrt{0.20556^2 + 1.22778^2} }{22000^2}\times 100 \)
\( \% Z = 2.5720 \)[%]
\( I_s = \displaystyle\frac{100}{2.5720} \times \displaystyle\frac{10\times 10^6}{\sqrt{3}\times 22000} \)
\( I_s = 17.7 \)[kA] となります。特段問題のない値ですね。
畢竟どういうこと?12.5kAの製品を選べば良い?
上述のように、高圧受電設備においては受電点短絡容量は必ず 160[MVA]、短絡遮断容量 12.5[kA] 以下となります。では、「考える必要性が無いのではないか」と思われる方もいらっしゃるかもしれません。「高圧受電地点」のみに関して言えば、その通りです。もちろん、コスト面を考慮して、計算上 8kA の短絡遮断容量の製品を選ぶこともできますが、あまりお勧めはできません。近年は再生可能エネルギーの増加の影響によって、短絡遮断容量が大きくなることもあり得るためです。
話がそれてしまいましたが、実は「主変圧器二次側(低圧側)」の短絡遮断容量においてさらに重要になるのです。私たちが通常使用する電圧帯の製品を守るために、短絡遮断容量を考えることは特に重要なのです。詳しく見てみましょう。下図のような設備を考えます。
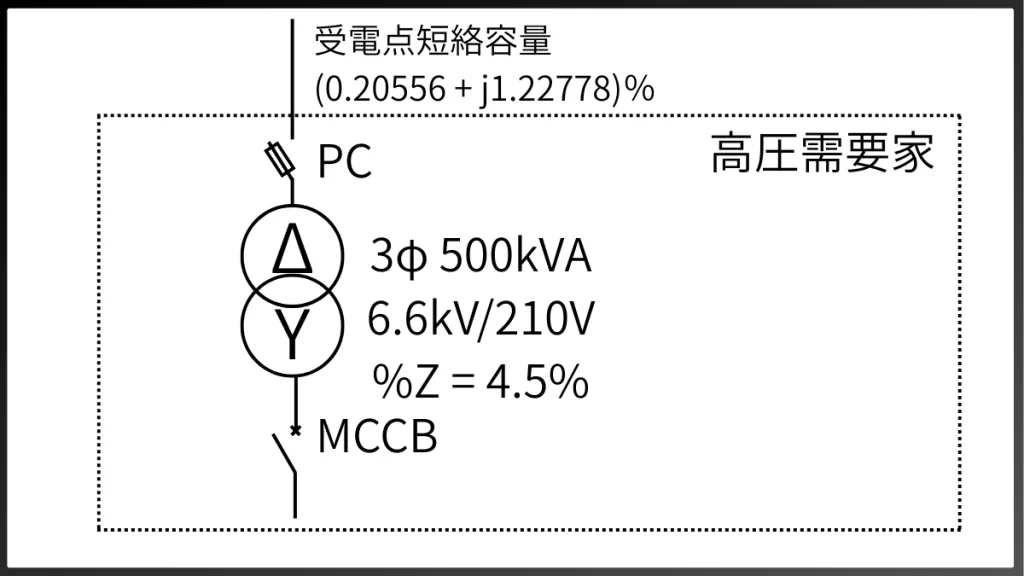
受電点短絡容量は、先ほどの電験三種の例題と同じ、\( %\dot{Z} = 0.20556 + j1.22778 \)[%] を採用します。また、主変圧器は 500kVA(6600/210V)、%Zは日立産機のモールド変圧器のカタログ値を参考に 4.5% を採用します。ここで「随分とインピーダンスが大きくなるので、大丈夫じゃないか」と思った方もいらっしゃるでしょう。T係長もその一人でした。気を付けましょう。変圧器メーカのカタログ値は変圧器容量を基準とした %Z の値です。先ほどの議論に繋げるためには基準容量をそろえる必要性があります。
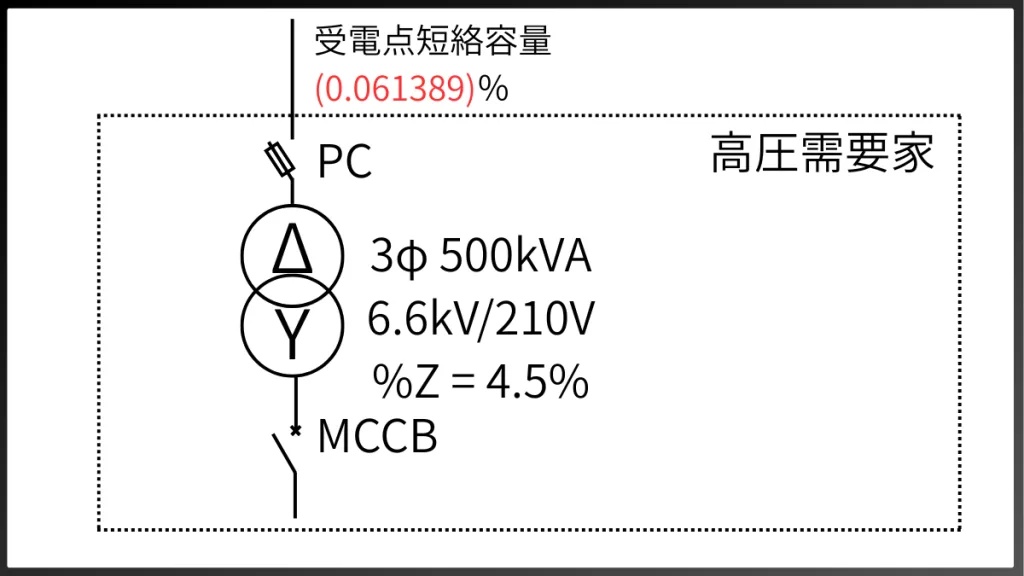
主変圧器二次側の短絡電流を考えるので、500kVA に換算する必要性があります。基準容量を換算するには、新しい基準容量を \( P_B \)、古い容量を \( P \) で表すとすると、
\( \% Z’ = \displaystyle\frac{P_B}{P}%Z \)[%] で求められます。
前述の受電点までの短絡容量は
\( \% Z’ = \displaystyle\frac{500\times10^3}{10\times10^6}\times 1.22778 \)[%]
\( \% Z’ = 0.061389 \)[%]
※実務では安全方向で考えるので、リアクタンス分に比べて非常に小さい抵抗分は除くことが多いので、今回はそのようにしています。変圧器も全てをリアクタンス分として考えます。
従って、主変圧器二次側で三相短絡事故が起きたとすると、上位側の %Z は
\( \%\dot{Z} = 4.5 + j0.061389 \)[%]
\( \%Z = 4.56139 \)[%]
となります。求める短絡電流は、
\( I_s = \displaystyle\frac{100}{4.56139} \times \displaystyle\frac{500\times 10^3}{\sqrt{3}\times 210} \)
\( I_s = 30.1365 \)[kA]
どうでしょうか?考えていたよりもずっと大きな短絡電流が流れる可能性があることが実感できたと思います。短絡遮断容量の選定を誤ってしまうと、短絡事故時にブレーカが燃え、事故電流が遮断できずに、最悪の場合、大規模な火災になってしまうのです。私たちプラント電気設備エンジニアの大きな責任です。
スポンサーリンク
短絡遮断容量は2種類あるの?
ブレーカのカタログを開くと、遮断容量の欄に Icu と Ics という二つの異なる数値が併記されていることに気づきます。一見すると似たような指標に見えますが、実務上の運用においては「事故の後にそのブレーカを再利用できるかどうか」という決定的な違いがあります。Icu(定格限界短絡遮断容量)は、いわばブレーカにとっての「究極の限界値」です。短絡事故という異常事態に対し、自らが損傷することを厭わず、とにかく回路を遮断して下流の設備や電線を守る能力を指します。試験上、一度遮断した後に再度投入して遮断できることが確認されていますが、遮断後の絶縁性能や通電能力は保証されず、基本的には交換を前提とした「使い切り」の性能と考えるのが安全です。
これに対して、Ics(定格サービス短絡遮断容量)は、より実用的な「継続使用」に焦点を当てた指標です。これは短絡事故を遮断した後でも、ブレーカとしての機能を維持し、そのまま再利用が可能であることを示しています。Ics の値が推定短絡電流を上回っていれば、万が一の事故後も清掃や点検を経て、部品交換なしで早期の復旧が期待できます。病院の電力供給ラインや工場の重要生産ラインなど、ダウンタイムを極限まで短縮したい場所では、計算上の短絡電流値を上回る Ics になるブレーカを選定することが、設備の信頼性を高める鍵となります。
設計実務において、どちらの数値を基準にすべきか迷う場面もありますが、一般的には、コストと安全性のバランスから Icu が計算上の短絡電流を上回ることを最低条件としつつ、重要度の高い回路には Ics を重視した製品を充てるという使い分けがなされます。「単に遮断できるか」だけでなく「遮断した後にどうなるか」という視点を持つことで、より一段上の設備設計が可能になります。カタログスペックの背後にあるこうした意味を理解しておくことは、事故発生時の復旧シナリオを想定する上でも極めて重要です。
まとめ:短絡遮断容量の選定は電気設備の安全を守る「要」
高圧需要家の設計において、短絡遮断容量の検討は単なる計算作業ではありません。受電点から末端のブレーカに至るまで、電気系統のあらゆる地点で想定される「最悪の事態」を数値化し、それに対抗しうる防壁を築く極めて重要なプロセスです。受電点では電力会社の規定に基づく12.5[kA] という基準がありましたが、主変圧器を介した二次側(低圧側)では、変圧器の特性によって想像以上に巨大な短絡電流が流れ込むことを、具体的な計算を通じて実感いただけたはずです。
実務においては、算出した短絡電流に対して遮断器の限界性能を示す Icu が上回っていることはもちろん、設備の重要度に応じて継続使用を担保する Ics にも目を向ける必要があります。また、将来的な系統の変化や変圧器の並列運転(パララン)の可能性、ケーブル長によるインピーダンスの減衰効果など、机上の計算式を超えた多角的な視点が、精度の高い設計には欠かせません。
「容量」という言葉の定義に違和感を覚えることもあるかもしれませんが、その数値が意味するのは、事故という暴力的なエネルギーから設備と人命を守り抜く「耐力」そのものです。電験三種の知識を実務の道具へと昇華させ、常に根拠を持った機器選定を行うこと。その積み重ねこそが、プラント電気設備エンジニアとしての信頼を築き、大規模な火災や波及事故を未然に防ぐ唯一の道となります。この記事が、皆さんの設計実務における確かな一歩となれば幸いです。


