はじめに
私たち電気エンジニアが日常的に扱う交流(AC)現象は、電験三種の理論科目における最大の難関の一つです。T係長も、初めての電験三種受験時には「理論」科目の壁に敗れました。特に、有効電力 (P)、無効電力 (Q)、皮相電力 (S) を求める電力計算では、数式だけを頼りにすると、どこかで符号を誤ったり、最終的な数値が現実の現象と一致しなかったりするミスが頻発します。
電験三種の計算では主に複素数が用いられますが、「無効電力(Q)をマイナスで扱うか、プラスで扱うかよく分からない」や「計算結果が現場の現象と結びつかない」という数式と実務の間のギャップこそが、計算ミスを生む根本的な原因なのです。このミスを劇的に減らし、交流回路の電力計算を確実な得点源に変える最強の武器が「ベクトル図」の活用です。この記事では、ベクトルを理解することが何故大切かを説明します。
ベクトル図の導入:電力計算における「最強の設計図」
ベクトル図の最大の利点は、交流の計算を単なる数値ではなく、「向き」と「大きさ」を持つ「矢印」として視覚化できる点にあります。この視覚化によって、L負荷であれば無効電力 (Q) のベクトルは必ず上向き、C負荷であれば必ず下向きになるという、現象が持つ絶対的なルールを常に目で確認できます。例えば、L負荷の回路を計算しているにもかかわらず、最終的に Q がマイナスになった場合、「ベクトル図で上向きになるはずの Q が下向きになっている!計算ミスだ!」と瞬時に検算が可能です。
また、ベクトル図は電圧 (V) と電流 (I) の位相差 (θ) を明確に示し、「遅れ」であれば基準ベクトルから時計回り(下向き)、進みであれば反時計回り(上向き)に描かれるため、複雑な複素数計算の途中で虚部の符号に悩まされることなく、位相の向きを正確に把握できます。
例えば、単相100VのR=10Ω、L=j15ΩのRL直列回路に流れる電流Iを考えて見ましょう。複素数計算をするのであれば、
\( I = \displaystyle\frac{100}{10+j15}\)
\( I = \displaystyle\frac{100(10+j15)}{10^2+15^2} \)
\( I = 3.08 + j4.62 \) となりますが、これが直感的に正解かどうか判断できますか?
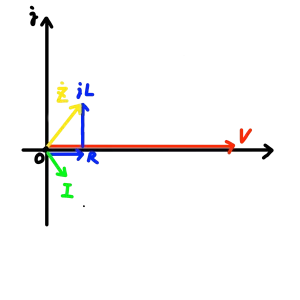
ベクトル図さえ理解していれば、簡単です。下記の図より、そもそも電流値は-jの領域ですから、計算ミスをしていそうなことが分かります。分子に\(10-j15\)を掛けるべきところを間違えていますね。正解は、\(I=3.08 – j4.62\)です。ベクトル図的にも間違いなさそうです。
実務応用:電力計算ミスが減る具体的なテクニック
このベクトル図の活用は、単なる電力三角形の描画に留まらず、電験二種や一種でも頻出する電力系統の現象理解にも不可欠です。交流回路におけるキルヒホッフの法則に基づく「電圧降下」の計算式は、複素数だけで処理するとミスしやすい箇所ですが、ベクトル図を描くことで、インピーダンス Z による電圧降下 (Z˙I) が、基準電圧 (Vr) に対してどのような「向き」で加わるかが一目瞭然となります。
特に、軽負荷時に力率が進み、電圧降下のベクトルが基準電圧側に倒れ込み、電源電圧 (Vs) が受電端電圧 (Vr) よりも大きくなってしまう「フェランチ現象」を、視覚を通じて明確に理解できます。「負荷が軽くなり、力率が進みになるとは電圧が上がる」という実務の経験則が、ベクトル図によって理論的に裏付けられることで、計算の正確性が飛躍的に向上するのです。
ベクトル図をマスターするための学習と受験テクニック
ここまで見てきたように、ベクトル図を習得することは、電験三種の合格に直結するだけでなく、高調波流出や系統連系といった高度な実務分野を正しく理解するために必須スキルです。このスキルを効率的に学ぶためには、単なる理論の教科書だけでなく、実務への応用を解説した書籍を活用することを強く推奨します。例えば、『実践 ベクトル図活用テクニック』のような書籍は、電力系統の電圧変動や保護継電器の動作原理など、現場の現象をベクトル図で分かりやすく解説しています。
また、受験対策としては、計算を始める前に、負荷の種類から電力三角形だけをさっと描く習慣をつけることが重要です。これと並行して、下記の記事で電卓操作テクニックを身に着け、計算処理速度と正確さを向上させれば、「理論」や「電力」科目の計算問題は確実な得点源となるでしょう。
まとめ:ベクトル図は「現象理解」の羅針盤
交流回路の電力計算でミスが激減する理由は、ベクトル図が「計算結果の物理的な妥当性」を常に視覚的にチェックさせてくれるからです。複素数計算が最終的な数値を求めるための手法であるのに対し、ベクトル図は「なぜその数値になったのか」という現象の裏付けを、実務的な感覚と結びつけるための手法です。
L負荷なら Q は必ず上向き(プラス)というシンプルな図的ルールを頭に入れるだけで、複雑な計算で生じる符号ミスや、不当な大きさのミスを即座に発見し、修正することが可能になります。実務経験豊富なあなただからこそ、この「現象理解の羅針盤」であるベクトル図をマスターし、電験三種の理論科目を自信を持って突破することが可能になるのです。より深く学びたいという方は以下の記事も合わせてご覧ください。




